I dag skal vi studere innsiden av Tetris-spillet skrevet under plattformen arduino og LED-matrise.
Forfatteren av dette hjemmelagde produktet er AlexGyver, forfatteren av YouTube-kanalen med samme navn. Velkommen til den fantastiske verdenen med firkantede piksler.
La oss starte med historien. Tetris er et spill der figurer bestående av 4 firkanter faller fra topp til bunn. I forskjellige kombinasjoner kan disse figurene roteres og flyttes til venstre og høyre. Målet med spillet er å samle horisontale nivåer som er ryddet og poeng blir tildelt deg. Å miste anses som øyeblikket når den nye figuren ikke har noe å falle. Tetris ble oppfunnet av den sovjetiske programmereren Alexei Leonidovich Pazhitnov.
Den opprinnelige Pascal-versjonen dukket opp 6. juni 1984. Siden den gang har Tetris kommet langt og blitt portert til alle plattformer som det generelt er mulig å spille spill, samt til enheter som ikke er beregnet på spill i det hele tatt, for eksempel en ingeniørkalkulator, et oscilloskop og, vil du ikke tro, et loddejern.
Med antall solgte kommersielle versjoner er Tetris overlegen alle andre spill i menneskehetens historie. For bare en Game Boy ble det solgt 35 millioner eksemplarer, for ikke å nevne det bærbare Brick Game, som nesten alle hadde på en gang.
Vi vil begynne implementeringen av tetris på arduino og en fargematrise med analysen av "krykker". Matrisen består av LED-farger med tre farger. Problemet med denne typen matrise er at den er for kul. Fargen på hver piksel er kodet med 24 biter, det vil si 8 biter for hver komponent: rød, grønn og blå. Det er ingen slike data om arduino, det er følgende - 32 biter.
Fargene på alle lysdioder skal lagres i RAM, da vi vil endre dem. Og i tillegg har vi for en matte på 16 med 16 nøyaktig 1 KB okkupert dynamisk minne, og arduino nano har bare 2 av dem.
Legg til noen flere biblioteker og begynn å skrive kode, minnet slutter. Forfatteren bruker i utgangspunktet ikke for eksempel arduino mega, der det er mer minne. Målet er å lage spillet spesifikt på arduino nano ved å bruke enkle, standard og kjente verktøy, men samtidig ikke-standard tilnærminger og "krykker" og med deres hjelp oppnå den mest optimale koden.
Den første "krykken" vil være avslaget på å lagre figurene til figurene og generelt alt som skjer på skjermen separat.Vi trenger å lagre koordinatene til punktene til fôringsfiguren og koordinatene til punktene til de allerede droppet figurene, det vil si at vi maksimalt trenger en annen gruppe, todimensjonal 16 x 16, og dette er så mye som 256 byte.
Du og jeg har allerede en rekke farger for alle piksler, la oss bruke den. Faktisk, i tillegg til at vi kan sette en farget prikk på matrisen, kan vi måle lyset på et eksisterende punkt slik at vi jobber med farger.
Tetris begynner med en fallende blokk, som styres av knapper og har 2 koordinater i matrikskoordinatsystemet. Det er veldig enkelt, vi bygger en tidsur, i henhold til hvilken blokken vil falle. Dette er forfatterens bibliotek, du kan lese på nettstedet.
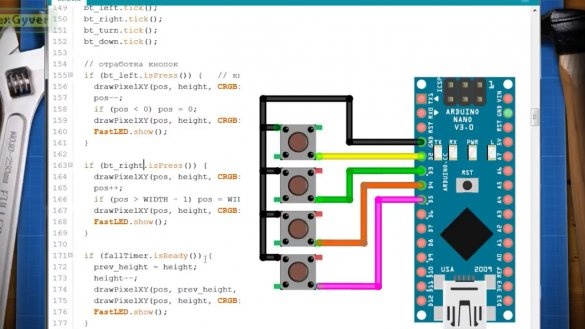
For å behandle knapper bruker forfatteren også biblioteket sitt. Tilkoblingsskjemaet til knappene er latterlig enkelt: 4 knapper, 8 ledninger.
Hvert trinn i tidtakeren tegner vi et punkt, en piksel under det gamle, og tegner det gamle punktet i svart, det vil si, slå av LED-en. Ved å klikke på knappen gjør vi det samme, men med en horisontal koordinat. Vel, for anstendighet, vil vi begrense størrelsen på matrisen slik at punktet ikke går utover feltet.
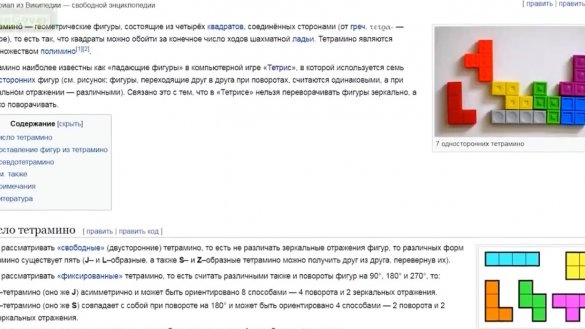
Ikke noe komplisert. Men dette er ikke så lenge fordi tiden er inne for å tegne tall. Vi vil jobbe som følger: vi vil beholde referansen til forsyningspunktet, som vi allerede har skrevet, vi vil kalle det hovedpunktet eller hovedblokken. Hovedblokken beveger seg i matrikskoordinatsystemet, vi har allerede gjort dette. Alle figurer av Tetris består av 4 blokker, og det er forresten den heter Tetris.
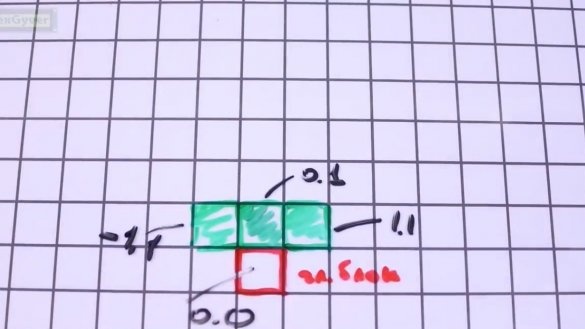
Følgelig gjenstår det å fullføre å legge til ytterligere 3 blokker i hovedblokken. La oss skrive koordinatene deres i koordinatsystemet til hovedblokken, slik at hovedblokken alltid er under. Det er veldig enkelt, ta figuren til det omvendte bokstaven T. Hovedblokken fra bunn til sentrum har koordinater 0.0 i koordinatsystemet.
Den øvre blokken er 0,1, den høyre er 1,1 og den venstre er -1,1.
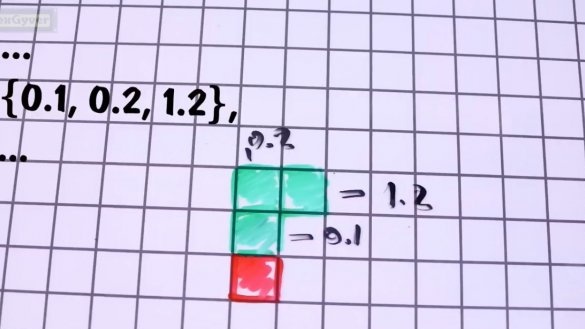
Ta bokstaven G. Den nedre blokken er 0,0, den neste 0,1, den neste 0,2 og kanten av bokstaven 1,2.
Vi skriver disse koordinatene i matrisen i følgende form: {0,1, 0,2, 1,2} og slipper matrisen i flashminnet for ikke å kaste bort dynamisk minne. Når det gjelder rotasjonen av figurene. Det er umulig å rotere figurene. Det er kornete det er veldig vanskelig å forklare for mikrokontrolleren hvordan du gjør dette. For å gjøre dette, må du stille rotasjonssenteret, på en eller annen måte dekomponere figuren i deler og se etter nye koordinater for hver del, under hensyntagen til sterk pikselering, noe som åpenbart vil føre til feil og det vil vise tull. Problemet er løst veldig enkelt, vi vil ha i minnet alle 4 posisjonene for alle figurer og alle.
Nå gjenstår det faktisk å velge figurtallet tilfeldig og tegne det rundt den fallende blokken. Her, for alle 3 gjenværende blokker, tar vi koordinatene fra flashminnet, oversetter dem til de globale koordinatene til matrisen og slår på lysdiodene. For øvrig er fargen også valgt tilfeldig fra de 6 mest enkle og lyse fargene på rgb-rommet. Rotasjonsvinkelen til figuren i begynnelsen av runden stilles også tilfeldig, og når du trykker på knappen opp, bare ta neste sett med koordinater for å tegne og rotere den med klokken. Å flytte en form fungerer på samme måte. Først sletter vi figuren i forrige posisjon, det vil si tegner den i svart, deretter i den nye stillingen tegner du den nåværende fargen på figuren. Når vi snur igjen, sletter vi den gamle stillingen og tegner bare en ny.
Firmware kan lastes ned kl. Vi vil bare analysere essensen. La oss starte med å sjekke venstre og høyre vegg og bunn. Alt er veldig enkelt med bunnen, vi ser på hvert trinn i høst, har baseenheten nådd en høyde på 0, dette er ikke vanskelig, men hver gang vi trykker på kontrollknappen, må vi se om det ekstreme punktet på formen til sideveggene til matrisen berørt.
Hvis du blir berørt, ikke flytt figuren. Det samme gjelder rotasjonen av figurene. For eksempel, hvis den nye plasseringen av figuren strekker seg utover veggene, er rotasjonen forbudt, og siden alle formene vi har er av forskjellige former, så er de ekstreme blokkene for dem alle forskjellige. Det ville være mulig å male individuelle ekstreme blokker for hver figur for å forenkle arbeidet med mikrokontrolleren, men la det bli vurdert at de oppfant det for dette.
Alt er veldig enkelt. Men neste oppgave er mye mer interessant. Vi må se etter kollisjoner med blokker som allerede ligger nedenfor.Hvis vi hadde en matrise som inneholdt tilstanden til alle cellene i feltet, ville det være enklere, men vi vil bruke en rekke farger for pikslene på båndet, så vi vil ha den kuleste "krykken". Hva er det faktiske problemet. Alt ser ut til å være enkelt, en grønn figur vil falle, og hvert fall i høsten, hvert skift til siden og hvert forsøk på å snu, bør sjekke om figuren i den nye stillingen hviler på de allerede liggende figurene. Hvis den omkringliggende fargen for alle blokker er lik svart eller lik fargen på figuren, tillater vi bevegelse i ønsket retning. Dette vil fungere til formen under oss har samme farge som den fallende formen. Det er faktisk "krykken": vi vil male den fallne formen i en annen farge på nytt. Mal om umerkelig for øynene, men merkes for programmet. Alt du trenger å gjøre er å øke lysstyrken på formens nåværende farge litt, og det er alt.
Figuren falt på bunnen eller en annen figur, lysstyrken økte ikke merkbart, og i den nye runden vil de fallende figurene ikke lenger forveksle fargen med sin egen, de vil falle på den og like faste, litt legge lysstyrken.
Forresten, når du trykker på knappen ned, suser figuren ned i høy hastighet og tar sin plass.
Vår Tetris sitter igjen med den siste touch, nemlig å sjekke og fjerne de fylte nivåene horisontalt. Alt er enkelt her. Etter å ha fikset figuren i den aktuelle runden, beveger vi oss langs linjene og sammenligner fargene på pikslene med svart. Hvis det ikke er en eneste svart piksel i hele linjen, vil vi tømme hele linjen.
De oppdagede linjene er fylt med hvitt, deretter synker lysstyrken gradvis til null og animasjonen oppnås. Videre blir alle piksler, fra den første fylte linjen til toppen, forskjøvet ned og antall linjer som er tømt. Denne prosessen gjentas til det ikke er fullførte nivåer. Vi sjekker også om vi har nådd toppen, noe som betyr å tape. I dette tilfellet vises en konto som er lik antall rensede nivåer.
Kontoen vises i numre, som er lagret i minnet som et sett med nuller, og lysdiodene blir deretter slått av eller på. Slik ser Tetris skrevet i adressematrisen ut. Takk for oppmerksomheten. Vi ses snart!
videoer: